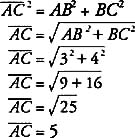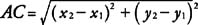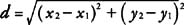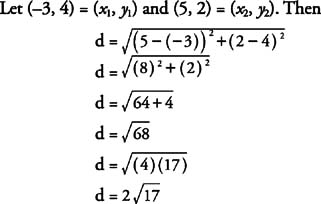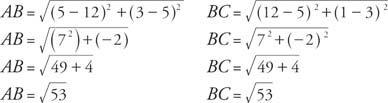To find the square root of a given number is to think of what number when multiplied by itself is equal to the given number.
For example, to find the square root of 4, we have to think of a number that when multiplied by itself gives 4. The number is 2 since 2 × 2 = 4.
So the square root of a given number is the positive number whose square produces the given number.
Properties of Square Roots:
- The product of two values in the square roots with different numbers inside it can be written in a single root in a product of those two root values.
- The number outside the square root symbol, when it gets into square root, it turns into a square of number.
- The square root of fraction value can be written as individual roots, as root in numerator and root in denominator separately.
- When a perfect square comes out of the square root symbol, it becomes the number without square root.
Square root is an radical symbol which is used in the mathematics. It is shown as the symbol as √. The number inside the radical symbol is called as the rubicund, for example if the given value is √x. The x is called as the rubicund which is the number inside the radical symbol √. There are more number of roots available depending upon the value we have. The roots are square root √x, cube root 3√x, Fourth root 4√x this up to nth root n√x. Here we are going to see about the square root of 16 and 17 in different methods of solving.
Let’s make it clear with some examples:
- √x * √y = √xy [By the first property]
- = x√y = √x2y [By the second property]
- √x/ y = √x/√y [By the third property]

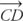 or
or 
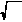 25) is 5.
25) is 5.