Basic understanding of reflex angles

To define reflex angle, let us look at the following figures:

What is it that is different about these angles? Or in other words, what do we notice about these angles? Note that the measures of all the angles are greater than 180 degrees. Based on this understanding we now define reflex-angles as follows: An angle whose measure is more than 180 degrees and less than 360 degrees is called a reflex angle. Mathematically that can be written like this: If an angle measure α is such that, 180 < α < 360 degrees, then α would be a reflex-angle measure.

Now that we know what a reflex-angle is, the next most obvious question would be how can a reflex-angle be measured? Considering the fact that normally we use a set square or a protractor to measure angles, we know that the maximum angle that can be measured using a protractor or a set square is 180 degrees. So how can we measure reflex-angles?

How to measure a reflex angle?
Every normal angle, which is not a reflex-angle, has its corresponding reflex-angle.  Whether an angle is acute or obtuse, it would always have its corresponding reflex-angle. This can be seen in the examples below:
Example 1: 

Here the acute angle is 49 degrees and the corresponding reflex-angle is 311 degrees. The sum of these two angles is 49 + 311 = 360 degrees.
Example 2: 

Here we have an obtuse angle measuring 112 degrees and its corresponding reflex-angle measuring 248 degrees. The sum of these two angles is 112 + 248 = 360 degrees.

Therefore based on the definition of reflex angle, we can state that the sum of an angle and its corresponding reflex-angle is always 360 degrees. Thus if we want to measure a reflex-angle, we follow the following steps:
1. First we measure the corresponding acute or obtuse angle (say 112 degrees or 49 degrees in the above figures) = α degrees.
2. Now subtract the angle thus measured from 360 degrees. Thus our reflex-angle
= r = 360 - α degrees.

Where do we find reflex angles?

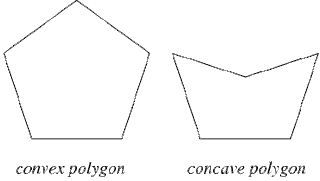
Reflex-angles are usually found in concave polygons.

A concave polygon would have at least one reflex-angle. Other examples of concave polygons are shown below:

Here we have a concave quadrilateral, a concave pentagon and a concave heptagon.

Geometry: Alternate interior angles

Definition: Alternate interior angles
Consider a pair of parallel lines is intercepted by a transversal. At each of the intersection points of the lines with the transversal, 4 angles are formed, making a total of 8 angles for the two lines. Each of these angles have a name or significance. Let us try to understand the following example of alternate interior angles.

The above figure shows two black lines intercepted by the red transversal. In the interior of the lines, four angles are formed namely, <5 a="a" also="also" alternate="alternate" and="and" angles.="angles." angles="angles" are="are" called="called" congruent.="congruent." green="green" if="if" interior="interior" is="is" of="of" other="other" p="p" pair="pair" similarly="similarly" the="the" these="these">
Theorem related to alternate interior angles:
When a pair of parallel lines is intercepted by a transversal, each pair of alternate interior angles thus formed are congruent. Therefore in the above figure, angle <5 and="and" angle="angle" congruent="congruent" is="is" p="p" to="to">
Examples of alternate interior angles:
The following pictures show examples of alternate interior angles:
Example 1:

In the above figure, the angles 76 and b are alternate interior angles. Therefore we can say that measure of angle b is 76. Similarly measure of angle a would be 104 since these two are also alternate interior angles and we know that alternate interior angles are congruent.

If one pair of alternate interior angles is acute, then the other pair of alternate interior angles has to be obtuse.  (Note an acute angle is an angle whose measure is less than 90 degrees and an obtuse angle is an angle whose measure is more than 90 degrees but less than 180 degrees)
Example 2:

In the above figure, the parallel lines are intercepted by a horizontal transversal. So here the purple dots are a pair of obtuse alternate interior angles and the pink dots are a pair of acute alternate interior angles. As we already know both the purple angles have to be congruent to each other and similarly both the pink angles also have to be congruent to each other.

Introduction to concept of median

What is median?
Median in math has two meanings. One is the geometric meaning and another is the statistical median.

Geometric median definition:
In a closed plane figure such as a triangle, the line segment that connects the midpoint of one side to the opposite vertex is called the median. See picture below:

The above picture shows a triangle ABC. D, E and F present on the sides AB, BC and CA, so that, AD = DB, CE = EB and AF = FC. The line segments AE, CD and BF are from the triangle ABC. The points where all the three geometric mid-segments intersect is called the centroid of the triangle also called the centre of gravity. In the above figure, O is the centroid of the triangle.

Statistical median definition:

In statistics it is a measure of central tendency. In a frequency distribution, the central value around which most of the values of the variable are centered is called the measure of central tendency. Of the various measures of central tendencies, the most popular are mean, middle number and mode. It is defined as middle value of the data set. For finding median we need to follow the following steps:

1. Arrange the data set in ascending or descending order.
2. If the number of entries is odd, then the middle value would be the (n+1/2)th value.
3. If the number of entries is even, then the middle value would be the average of the (n/2) th and the (n/2 + 1)th value.
4. The value found in step 2 or 3 is called the middle number value.

Sample problem:
1. Find the middle number of the following data set of marks obtained by 10 students in a class test of maximum 10 marks: 8, 8, 9, 5, 5, 6, 6, 7, 6, 4
Solution:
Step 1: Arrange the data in ascending order: 4, 5, 5, 6, 6, 6, 7, 8, 8, 9
Step 2: The number of entries is 10 which is an even number, so we move to step 3.
Step 3: The two middle values would be 10/2 = 5th and 10/2 + 1 = 5+1 = 6th value. Both these are 6. Therefore the middle number is 6.

Elementary math concepts

Elementary math covers all the basic operations, function and concepts in algebra. In elementary math is the main part covered is arithmetic operations. All the basic operations are presented in this area. This is covering all basic operation of addition multiplication, subtraction, and division. The elementary algebra covers all concepts from kindergarten level to middle school level. This is also help to solve for real life math problem.

Example: 4x+ 2 = 1

Elementary Math Concepts Covers:

Elementary math concepts contain this basic operations

Arithmetic Operations:

The real numbers have the following properties:

a + b= b +  a    ab  = ba                            (Commutative Law)

(a+ b)+ c= a+ (b + c)      (ab)c = a(bc)        (Associative Law)

a+(b +c)= ab +ac                                       (Distributive law)

Fractions:

To add two fractions numbers with the same denominator, we use the Distributive Law property:

a/b+c/b= 1/b*a+1/b*c  =1/b(a+c)  =a+c/b

To add two fraction with different denominators, we use a frequent denominator:

a/b+c/d =  ad+bc/bd

Factoring

Here we can make use of Distributive Law to increase certain algebraic conditions. In rare case we need to repeal this method (again using the Distributive Law) by factoring an expression as a product of simpler ones. The easiest condition occurs when the given expression has a common factor as given below...

3x(x-2)=3x2 – 6

Elementary Algebra Concepts Problems

Q 1 :   Find the larger number, -13 or -16?

Sol :  If a number has a negative sign, we dont conclude the number by ony seeing the value, here we have to consider the negative sign. If the value of a number with negative sign increases, the actual value of the number is decreses.

-16,-15,,-14,-13,-12,-111,-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0

so,-13 is larger than -16.

Q 2:  List all the integers between -2 and 4.

Sol :     -2,-1, 0, 1,2,3,4 these number are present in the -2 ,4

The -2, 4 between numbers are -1,0,1,2,3

Q 3:  Reduce 14/35.?

Sol :      14/35

We divide 7 on both sides

2/5

Q 4: Simplify 8 -: 2//3?

Sol :  We divide the given equation this is simple method the division inverse of multiplication

8

4*3   = 12

Q 5:  Simplify 1/2 + 2/3?

Sol  :      1/2+ 2/3

We take L.C. M   on 2, 3

1*3/2*3 +2*2/3*2

=3/6+4/6 =3+4/6

=7/6

Q 6.12x=4?

Sol :    x=4/12

x=1/3

Q 7:    3X+4y=5x-2y ?

Sol :         4Y+2y=5x-3x

6y=2x

y=2x/6

y=x/3

Q 8 :  x-4=8?

Sol : We add +4 on both sides

x=8+4

x=12

Q 9:  Factorize the given expression x2-9   ?\

Sol :  The general form of

(a2-b2)=(a-b)(a+b)

So, x2-9=  (x-3)(x+3)

Adjacent Angles

Definition for Adjacent Angles states that two angles are said to be adjacent, if:
• Both the angles are formed using the same side
• Both the angles have a same corner point i.e. the vertex
• Both the angles do not overlap on each other i.e. they should not have any interior point in common.

In simple words, Adjacent Angles Definition states that angles that are formed side by side using a common ray coming out of a common vertex in such a way that the common ray is between two other rays that forms the angles without any overlapping.

If two angles are given, they are said to be adjacent if they are only as per the Definition Adjacent Angles has stated.  There are certain scenarios when two angles do not satisfy the conditions stated in the Adjacent Angles Definition, they are:
1. Two angles share a common corner point or vertex but do not share a common side.
2. Two angles share the same side to form the angles, but do not have a common point at one of its corners.
3. Two angles given, in which one angle overlap the other.
The above cases that do not satisfy the conditions stated in the definition of adjacent angles can be declared as not adjacent. So these angles are not adjacent to each other.

Example of Adjacent Angles
An example of Adjacent-Angles helps to understand the concept in a better way. Consider three rays A, B, C coming out of the common vertex O. Two angles namely Angle x and Angle y are formed in such a way that angle x is formed between the sides OA and OB whereas angle y is formed using the sides OB and OC.  Here the vertex O is used as common and the side OB is used in common to form both the angles.

Adjacent Angles as Complementary Angles
When there are two adjacent-angles given with common vertex and common side, find the sum of the two angles.  If the total of the two angles is ninety (90) degrees and if it forms a right angle, then these adjacent-angles are said to be complementary and are termed as complementary angles. We can call it as adjacent complementary angles too.

Adjacent angles as Supplementary Angles
If two adjacent-angles are given, we can say that these adjacent-angles are supplementary angles if the total of the two adjacent-angles given is hundred and eighty (180) degrees and forms a straight angle. We can call it as adjacent supplementary angles.

Hypotenuse of a Right Triangle in brief

There are different types of triangle which we have learnt; one of them is the right angled triangle in other words a right triangle. A triangle in which one of the angles is a right angle that is 90 degrees is called a right triangle. The longest side of a right triangle is called the Hypotenuse of a Right Triangle and the other two sides are called the legs of the right triangle. We use the Pythagorean Theorem in finding the hypotenuse of a Right Triangle. The Pythagorean Theorem states that ‘the sum of the squares of the two sides (legs) of a right triangle is equal to the square of the hypotenuse’. Let us assume the lengths of the legs of a right triangle to be ‘a’ and ‘b’ units and the hypotenuse length to be ‘c’. By using Pythagorean Theorem, we can calculate the hypotenuse of a right triangle,
(Hypotenuse) ^2 = (sum of the squares of the sides (legs)^2
  c^2 = (a^2 +b^2)

This gives us the Hypotenuse of a Right Triangle formula, c = sqrt(a^2 + b^2)
Given the lengths of the sides or legs of a right triangle as 3 cm and 4 cm respectively, find the hypotenuse of the right triangle.  Here we are given the lengths of the two sides a = 3cm and b = 4cm, we need to find c. let us apply the Pythagorean Theorem, we get, c = sqrt(a^2+b^2). a^2= (3)^2 = 9 and b^2 = (4)^2 = 16, that gives us a^2+b^2 = 9 +16 = 25. So  c = sqrt(25) = +/- 5 , as length cannot be negative, the hypotenuse of the given right triangle is 5 cm.

Let us now learn how to calculate the Hypotenuse of a Right Triangle using the Pythagorean theorem given by hypotenuse = sqrt[(sum of the squares of the sides or legs)^2]. A ladder is placed against a wall of height 12 ft. The distance between the base of the ladder and the wall is 5ft, find the length of the ladder. In this problem, the triangle formed by the wall, the floor and the ladder is a right triangle and hence the length of the ladder would be the hypotenuse which we need to find. We are given the two lengths of the sides of the triangle which are 12ft and 5 ft respectively. We know c= sqrt(a^2 +b^2); here a = 12ft, b = 5 ft which gives us a^2 = 144 and b^2 = 25. So, c = sqrt(144 +25) = sqrt(169) = +/-13. The length of the ladder is 13 ft

Solving fourth grade math homework

In this article we are going to discuss about the mathematical concepts for fourth grade students. The students of fourth grade learn the different areas of mathematics, like place values of six digits numbers, expanded notations, place value chart, addition, subtraction, multiplication and division of three and four digits numbers, multiples and factors, HCF and LCM. Grade fourth students also learn unitary method, fractions, decimal numbers and measurement of time, length, mass and capacity.

Here we are going to discuss about some of them. This article will be helpful in solving fourth grade math home work.

Topics of Solving Fourth Grade Math

Some of fourth grade mathematical topics are as follows:

Place value: To read and write large number easily, the Indian place value chart is divided into periods as shown below:

Practice Questions: 

(1)Write the number name of these numbers:

(a)    2, 50,946 = Two Lakh fifty thousand nine hundred forty six.

(b)    6, 92,438 = Six lakh ninety two thousand four hundred thirty eight.

(c)    20, 10,101 = Twenty lakh ten thousand one hundred one.

 (1)   Write the numeral of these number names:

(a)    One lakh fifty thousand two hundred eighteen = 1,50,218

(b)   Nine lakh ninety five thousand sixty three = 9,95,063

(c)    Seventeen lakh fifteen = 17,00,015

Simplification involving four fundamental operations: 

In this lesson we will learn to use all the operations together. The fourth grade learners are able to learn the order of operations through this section.

Step 1 ---- Of

Step 2------Division

Step 3 ------ Multiplication

Step 4 ------ Addition

Step 5 ------ Subtraction

 So the order of operation is ODMAS.Now we will do some simplification using ODMAS rule:

 Practice Questions:

(a)    Simplify 36÷ 6 x 4 + 2 – 8

                   = 6x 4 + 2 – 8

                   =   24 +2 – 8

                    =    26 – 8 =18 Ans.

(b)   Simplify 6 + 8 ÷2 -2 x 1 + 5 of  2÷ 5

                    = 6 + 8 ÷ 2 – 2 x1 + 10 ÷5

                    = 6 + 4 – 2 + 2

                    = 12 - 2 = 10 Ans.

Now simplify these questions:

(a)    23741 -  3826 ÷  2 x 6 + 221

(b)   529 x 71 – 630 of 6 ÷ 3 + 4

(c)    6000 +9000 ÷  500 of 6 – 2000

(d)   6699 ÷ 33 +3075 ÷ 25 – 203

Answers: (a) 12484 (b) 36303 (c) 4003 (d) 123

Solving Fourth Grade Math Homework-unitary Method

Some basic knowledge is very important for fourth grade learners like:

• We have to add when we find the total cost of things tat we purchase.
• We have to subtract when we take back the balance.
• We have to multiply to calculate the cost of more articles.
• We have to divide when we find the cost of one.

Practice Question: 

If the cost of 25 Milton jugs is Rs. 8,250.  What is the cost of 48 such Milton jugs?

Solution: The cost of 25 Milton jugs = Rs.8, 250

                The cost of 1 Milton jug is Rs.8, 250 ÷ 25 = Rs.330

                The cost of 48 Milton jugs = Rs. 330 x 48 = Rs.15840

 Solve these problems: 

 28 digital diaries cost Rs.70, 560. What is the cost of 15 such diaries?

 Answer: 37,800

Statistics homework answers

Statistics is the branch of applied mathematics which deals with scientific analysis of data. The subject statistics had been started in early days as arithmetic to aid a ruler who needed to know the wealth of his subjects to levy new taxes. Now a days statistics  plays an important role in all organizations in their decision-making and planning. Statistics homework deals with mean,median and mode.

Classification of Statistics Homework Answers:

In statistics homework answers has following topics are

• Arithmetic mean
• Median
• Mode

The arithmetic mean;

In Statistics the arithmetic mean (A.M) or simply the mean or average of n observations x1, x2, …, xn is defined to be number x such that the sum of the deviations of the observations from x is 0.

         x1 +x2 +x3.......xn
x =  --------------------
                     n

the symbol Σ, called sigma notation is used to represent summation.

x=Σ xi
   -------
      n

Homework Example:

Calculate  mean of the data 9, 11, 13, 15, 17, 19.

Sol :

X =   Σxi/n = `[9+11+13+15+17+19]/[6] ` =` [14]/[6]`

Median :

Median is defined as central most or middle value for given series of data it should be arranged in ascending or descending order.

Homework Example:

Find the median of 23, 25, 29, 30, 39.

Sol:

The given values are already in  ascending order. No. of observations N = 5.

So the median = ` (N+1)/(2)`  =`(5+1)/(2)`
= 3 rd term =29
∴ Median = 29.

Mode:

In Statistics answers,Mode is also a measure of central tendency.

In a set of each observations, mode is defined as value which occurs most often.

If the data are arranged in the form of a frequency table, the class corresponding to  greatest frequency is called  modal class.

Homework Example:

Find the mode of 7, 4, 5, 1, 7, 3, 4, 6,7.

Sol:

Arranging the data in  ascending order, we get 1, 3, 4, 4, 5, 6, 7, 7, 7.

In above data 7 occurs several times. Hence mode = 7.

Homework Problems and Answers for Statistics:

Calculate mean :    
Problem 1:
Calculate the mean of the data 7, 12, 18, 14, 19, 20.
Problem 2:
Calculate the mean of the data   16,18,14,15,21,30,26,44
Problem 3: 
Calculate the mean of the data   22,77,55,11,22,26,38,72
Answers:
1) 15
2) 23
3) 40.35

Calculate median:
Problem 1: 
Find the median of 3, 4, 10, 12, 27, 32, 41, 49, 50, 55, 60, 63, 71, 75, 80.
Problem 2:
Find the median of 29, 23, 25, 29, 30, 25, 28.
Problem 3: 
Find the median of 26, 25, 29, 23, 25, 29, 30, 25, 28, 30.
Answers:
1) 49
2) 28
3) 27

Calculate mode:
Problem 1:
Find the mode of 12, 15, 11, 12, 19, 15, 24, 27, 20, 12, 19, 15
Problem 2:
Find the mode of 3,5,8,3,9,3
Problem 3: 
Find the mode of 3,5,8,5,6,7
Answers:
1) 12 and 15
2) 3
3) 5
 Follow my blog with Bloglovin

An Introduction to Calculating the Area of a Right Triangle

The Area of a Right Triangle
A Right Triangle or a Right Angled Triangle is a triangle which has right angle or 90 degrees as one of its interior angles. We have two types of Right Triangles namely, scalene right triangle in which one angle is right angle and the other two are unequal angles and the corresponding sides are also unequal. The other type is the Isosceles Right Triangle in which one angle is right angle and the other two angles are equal and also their corresponding sides are of equal length.  A right triangle is very useful in trigonometry, a branch of mathematics. Area of a triangle is given by half times the base times the height of the triangle. We can deduce the formula for Area of a Right Triangle using the following method. Let us consider a rectangle of length l cm and width w cm. Let us now cut the rectangle into two equal halves diagonally as shown in the figure below.

 
The triangles ABC and ADC are congruent triangles which means when placed one over the other they overlap exactly. Also they are right triangles with 90 degrees as one of their angles. They are of the same size and hence we can say that they have the equal area. From this it is clear that the area of a right triangle will be half the area of the rectangle.
The Area of the right triangle = ½ [Area of the Rectangle]
               = ½ [length x width]
             = ½ [l w]

From the figure, we can see that the length of the rectangle is one of the sides of the triangle which is called the base of the triangle. So, we have base of the triangle equals length of the rectangle.  Also the distance from the vertex A of the triangle ABC to the vertex B is the height of the triangle ABC which is the width of the rectangle. So, we have height of the triangle equals width of the rectangle. Substituting these in the above equation, Formula for Area of a Right Triangle = ½ [base x height]. So, to calculate area of a right triangle we use the formula ½ times [base x height]
Calculate the Area of a Right Triangle with base and height 12 cm and 17 cm respectively
Solution:  Base of the right triangle   = 12 cm
         Height of the right triangle = 17 cm
       Area of the right triangle   = ½ x base x height
                      = ½ x 12 x 17 = 6 x 17 = 102 cm^2

Characteristics of Right Angle Triangle

Triangle is a basic shape in geometry. A right triangle means 90 - degree angle that is one angle is right angle. It also called as right angled. It shows the relations between the sides and angles of a right triangle and it is the basic concept of trigonometry. The opposite side of the right angle is known as hypotenuse. The adjacent side to the right angle is known as legs or sometime known as catheters. This phenomenon is the basis of Pythagorean triangle theorem. This theorem states that the length of all three sides of a right triangle are integer and the side length are known as Pythagorean triple.

The basic principle properties of a right triangle are area, altitude, Pythagorean Theorem, inradius and circumradius. First we discuss about area of a right triangle. Area of a right triangle is equal to the one half of the base multiplied by the corresponding height. It is true for all right angled triangles. In a right triangle from the two legs if one leg is taken as a base then other leg is taken as height. So in other way we can say that area of a right triangle is one half of the product of the two legs means one half products of base and height. Mathematically suppose in a right triangle two legs are (a) and (b) and hypotenuse is (c) then formula for the area of a right triangle is expressed as [A=(1/2 ab)].

For finding area of a right triangle we have to calculate perimeter also. The formula we can see above. Suppose in a right triangle two legs (a=5) and (b=12) where a is base and b is height. Hypotenuse (c=13) is given. We know the formula area of a right triangle so we substitute all the values in formula. Finally we get area= (1/2 *5*12) = (1/2*60) =30 and unit of right angle triangle is square meter or square centimeters.

Similarly we can find surface area of a right triangle.  Formula for surface area of right angle triangle is [Area (A) =bc/2] where (a=√b^2+c^2), (b=√a^2-c^2) and (c=√a^2-b^2). Suppose for above problem we have to find surface area. We substitute all the values in formula that is (A=12*13/2).
From the right angle triangles we also find the Pythagorean Theorem. It is very useful in all parts of mathematics. It states that in any right angle square of hypotenuse is equal to sum of square of base and square of height that is (c^2=a^2+b^2).

Trigonometric equations

Trigonometric equations
In this article we shall study some basics of how to solve trigonometric equations. A trigonometric equation is an equation that involves trigonometric ratios in addition to algebraic terms. As trigonometric  functions are many to one type of functions, it is quite possible that such trigonometric- equations may have many roots (solutions).

This can be made clear by solving trigonometric equations examples:
For instance, sin ( pi/6) = ½ but the equation sin x = ½ has not only the solution x =  pi/6, but also x = 5 pi/6, x = 2 pi +  pi/6, x = 3 pi -  pi/6 etc. Thus, we can say that x =  pi/6 is a solution of sin x = ½ but it is not the general solution of the equation.

A general solution gives all the roots of an equation. When attempting to solve trigonometric equations online it is very imperative that the equations fed in are valid. For example, and equation like sin x = 2 would not have any solution. That is because we know that the range of the sine function is [-1,1]. So for any value of angle x, the value of sin x can never be = 2. Therefore the solution of such an equation would be : no solution.

The objective should be to develop methods to find general solutions of trigonometric-equations.
We know that sine, cosine and tangent functions are all periodic. Sine and cosine functions have a period of 2 pi and the tangent function has a period of  pi. Therefore the general solutions of the equations, sin t = 0, Cos t = 0 and tan t = 0 can be found as follows:
Sin t = 0 ? t = k pi, k belongs to the set of integers ------------- (1)
Cos t = 0 ? t = (2k+1)/2, k belongs to set of integers ----------- (2)
Tan t = 0 ? t = k pi, k belongs to the set of integers -------------- (3)

These results can be used to solve the general trigonometric-equations which are as follows:
Cos t = a, |a| = 1
Sin t = a, |a| = 1
Tan t = a, a’ belongs to set of all real numbers.
By solving a trigonometric equation we intend to find a set of solutions for the given set of trigonometric-equations such that each member of the solution set satisfies the set of equations.

Learn more about how to solve Trigonometry Problems.

Limit of a function

For understanding the limit of a function we must know the fundamental concepts of calculus and analysis which belonging to that particular function near a define input. In another way we can simplify by taking a simple example. Suppose function is f(x) and limit is x tends to c where c is a constant, then it means that function f(x) is get closer to limit as x get closer to c. more accurately when function is applied to each input , the result in an output value that is close to limit.

Limits of a sequence
As we know about the limits. Limits of a sequence means a value in term of sequences. If limit value exist then such sequence occurs. Limits of a sequence of any function can be understood by applying the function on a real line. This is one way to know the limits of function in term of sequence.

Limits of sequences
For knowing the limits of sequences we choose such type of example where limits value exist then the sequences will convergence. Limits are first apply for the real numbers and then for others such as metric spaces and topological spaces.

Limits of functions
In limits of functions we take any calculus function like additive or subtractive functions, because for simplify purpose these functions are easy. Functions are with limits where in limit x is approaches to any real number. When we solve such function in last we must put the limits. So in limits of functions output result are moves according to limits.

Limit of sequence
In limit of sequence, first take a sequence such as (Xn) with limit where x is tens to a and a is a constant. When we apply limit to this function if and only if for all sequences(Xn) means with (Xn) with all value of n but not equal to constant a.

Limits of a function
Limits of function means limits should apply to a function. Function may be different types. In limits of function we explain that what it means for any function which tends to real number, infinity or minus infinity. Limits of function can be both right handed and left handed.
Suppose in any case if both right hand and left hand limits of  function as x approaches to constant exist and are equal in value, their common value evidently will be the limits of a function. If however either or both of these limits do not exist then the limits of a function does not exist.

Triple integral solver

We know that when solving double integrals, we divide the two dimensional region into very small rectangles. Then we multiply the area of the rectangles with the value of the function at that point. Then we sum up these areas and then apply the following limit: lim (size of rectangle -> 0). Doing all that gives us the double integral of the said function.

Let us now try extending this concept to three dimensions. Just like in double integrals we had some region in a plane (say the xy plane), in triple integral we will consider a solid in space (i.e. xyz space). Just like in double integrals we had split the region into rectangles, in solving triple integrals we break down the solid into numerous rectangular solids (or cuboids). Extending further on same lines, just like how in double integrals we multiplied the value of the function by the area of the respective rectangle, in a triple integral example, we would multiply the value of the function at each of the point by the volume of the rectangular solid at that point. Instead of the limit of size of rectangle tending to zero, in case of triple integrals we have the limit as the volume of rectangle tending to zero.

With that we come to the definition of a triple integral. Which is like this: Triple integral is defined as the limit of the sum of product of volume of rectangular solids with the value of the function.
We call the double integral as an equivalent to double iterated integral. In the same way we can understand the triple integral as a triple iterated integral.

Symbolically the definition of a triple integral can be stated as follows:
Consider a function f(x,y,z). It is of three variables. It is continuous over any solid S. Then the triple integral of this function over the solid S can be symbolically stated as:

where the sum is taken over all the rectangular solids that are contained in the solid S. The limit is for the side length of the rectangles.
The above definition of triple integrals is useful only when we are given a set of data in the form of a table of values of volume and value of function. When a function is defined symbolically, then we use the Fubini’s theorem to solve triple integral examples.

First and Second Fundamental theorem of calculus

First Fundamental Theorem of Calculus: If f is continuous on [a, b], then F(x) = integral a to x f(t) dt has a derivative at every point of [a, b] and dF/dx = d/dx integral a to x f(t) dt = f(x), a is less than and equal to x is less than equal to b. Let us understand Proof of Fundamental Theorem of Calculus: We prove the fundamental theorem of calculus by applying the definition of derivative directly to the function F(x).

This means writing out the difference quotient F(x + h) – F(x) /h and showing that its limits as h approaches to 0 is the number f(x). When we replace F(x + h) and F(x) by their definite integrals, the numerator in above equation becomes F(x + h) – F(x) = integral a to x+h f(t) dt – integral a to x f(t) dt. The additive rule for integrals simplifies the right hand side to Integral x to x+h f(t) dt So that the above equation becomes  F(x + h) – F(x) /h = 1/h [F(x + h) – F(x)] = 1/h integral x to x+h f(t) dt. According to the mean value theorem for definite integrals, the value of the last expression in the above equation is one of the values taken on by f in the interval joining x and x + h. That is for some number c in this interval, 1/h integral x to x + h f(t) dt = f(c).

We can therefore find out what happens to (1/h) times the integral as h approaches to 0 by watching what happens to f(c) as h approaches to 0. As h approaches to 0, the endpoint x + h approaches x, pushing c ahead of it like a bead on a wire. So c approaches x, and since f is continuous at x, f(c) approaches f(x) .Lim h approaches 0 f(c) = f(x).Going back to the beginning, then we have dF/dx = lim h approaches to 0 [F(x+h) – F(x)] /h= lim h approaches 0 1/h integral x to x+h f(t) dt = lim h approaches 0 f(c)= f(x). This concludes the proof.

Let us more understand this through Fundamental Theorem of Calculus problems: let us take few fundamental theorem of calculus examples .suppose we have Find dy/dx if y = integral 1 to x^2 cos t dt.

Now to understand this solution suppose let us notice that the upper limit of integration is not x but x^2. To find dy/dx we must therefore treat y as the composite of y = integral 1 to u cos t dt and u = x^2 and apply the chain rule: dy/dx = (dy/du).(du/dx) = d/du integral 1 to u cos t dt . du/dx = cos u . du/dx= cos x^2 . 2x = 2x cos x^2.

Second Fundamental Theorem of Calculus: If f is continuous at every point of [a, b] and F is any anti-derivative of f on [a, b], then Integral a to b f(X) dx = F(b) – F(a). Let us understand this by second Fundamental Theorem of Calculus Examples suppose we have Evaluate integral 0 to pi cos x dx. Now let us solve this integral 0 to pi cos x dx = sin x 0 to pi = sin pi – sin 0 = 0 – 0 = 0.

Derivative of Logarithmic Functions

Derivative of Log Function
An exponential function is given by y=b^x, an inverse of an exponential function is given by x=b^y. The logarithmic function with base b is the function given by y=log x with base b where b>1 and the function is defined for all x greater than zero. The system of natural logarithm has a number e as its base. We know that the natural logarithms functions and natural exponential functions are inverses. If f(x) and g(x) are inverses of each other then the derivatives of inverses is given by g’(x)=1/f’[g(x)].So, the Derivative of Log Function can be found using the definition of derivatives of inverses as follows, given
f(x)=e^x and g(x) = ln x then, g’(x) = 1/f’[g(x)]
                                     =1/e^[g(x)]
                     = 1/e^ln(x)                 [g(x)=ln x]
                     = 1/x
So, the Derivative of Log Function is, d/dx[ln x]=1/x where x is greater than zero

Derivative of Log Base a of X 
We can find the Derivative of the general logarithmic function by the method of change of base formula.
 Log base a of x  can be written as ln x/ln a.
 Differentiating on both sides gives,
d/dx [log base a of x]= d/dx [ln x/ln a]
                                        =1/ln a . d/dx [ln x]
                                = 1/x ln a
Derivative of Log Base a of X is given by, d/dx[log base a of x] =1/[x ln a]
For example, find the derivative of log base 2 of x .
By the base change formula, we get, log base 2 of x = ln x/ln 2
Taking the derivative on both sides, d/dx [log base 2 of x] = d/dx [ln x/ln 2]
Here, ln 2 is a constant. On simplifying, we get, 1/ln 2 . d/dx [ln x]  
We know that derivative of ln x is 1/x. Substituting this value, we get
                        d/dx[log base 2 of x] = 1/[x ln 2]

Derivative of Log Base 10
Logarithms to base 10 are called the common logarithms. Common Logarithm is written as log x which means log base 10 of x.  Given y=ln x its inverse is given by e^y = x. Let us find the Derivative of Log Base 10 by taking derivatives on both sides with respect to x, d/dx [e^y] = d/dx[x] which gives  e^y dy/dx = 1. We have e^y= x, substituting this value, we get x dy/dx=1. We need dy/dx, so we shall divide on both sides with x which gives, dy/dx = 1/x. Derivative of Log Base 10 is given by, d/dx [log base 10 of x] = 1/x

Inverse Trigonometric Functions

Consider a function f(x)=(x+2), we can write this as y=x+2. Solving for x, we get, x = y-2. Interchanging the x and y terms gives a new function y=x-2, consider this as g(x). This new function g(x) is the inverse function of f(x). Inverse function is denoted as f^-1

Inverse Trigonometric Functions
Let us assume a given radian angle pi/2, we can evaluate a trigonometric function sin(pi/2)  equals 1. Inversely, if we are given 1 as the value of a sine function, then we can arrive to the radian angle y. Equating,  sin(pi/2) = 1, the radian angle for which the value of sine is 1 is pi/2. We can now write the inverse trigonometric function of sine as arc[sin(1)]= pi/2. In general, given the value x of the trigonometric function we can write the inverse trigonometric function as arc[sin(x)], arc[cos(x)],arc[tan(x)], arc[csc(x)], arc[sec(x)], arc[cot(x)] to name the radian angle that has the value x in each case.

Using the derivatives of inverse trigonometric identities we can obtain inverse trig functions integrals:

Integral[du/sqrt(a^2-u^2)] = sin^-1[u/a] +c
Integral[du/(a^2+u^2)=1/a[tan^-1(u/a)]+c
Integral[du/u[sqrt(u^2-a^2)]=1/a[sec^-1mod(u/a)] +c;
where u is a function of x, which is written as u=f(x)

How to Solve Inverse Trig Functions
Steps involved to solve inverse trig function, arc tan(-1):
Step1:  let y=arc tan(-1)
Step2:  tan (y) is -1 when pi/2<=y<=pi/2 [finding the interval]
Step3:  determine the radian angle of tan that gives the value of 1, which is pi/4
Step4:  determine the radian angle for a negative value, we know that tan(-x)=- tan(x)
Step5:  we get, tan y = -1
Step6:  the required radian angle is y = pi/4

Inverse Trig Functions Problems
Evaluate arc cos(-1/2)
Let y = arc cos(-1/2), we need to find the radian angle y
cos(y) = -1/2 , we know that pi/3 radian angle of cos gives the value 1/2. But here we have -1/2
We know that, cos(pi-x) gives us –cosx.
So, cos(pi-pi/3) = -1/2
We get, y=pi – pi/3 = 2pi/3 is the required radian angle

How to Graph Inverse Trig Functions
To graph inverse trig functions, first we need to understand the domain and range of the inverse trig functions which are:
Function Domain Range
y=arc sin(x)  -1<= x<= 1    -(pi/2)<=y<=(pi/2)
y=arcos(x)   -1<= x<=1   0<=y<=pi
y=arctan(x)   -infinity
y=arccsc(x)  x<=-1or x>=1  -pi/2<=y<=pi/2, y not equals zero
y=arcsec(x)   x<=-1 or x>=1  0<=y<=pi, y not equals pi/2
y=arccot(x)      -infinity  0

Plug in different values of x (within the range) to arrive to the respective y values of the given inverse trig function. Plot the coordinates (x,y) on the graph and join them. The curves thus obtained is the graph of given inverse trig function.

Introduction to standard deviation

Standard deviation

The most comprehensive descriptions of dispersion are those that deal with the average deviation from some measure of central tendency. Two of these measures are important to our study of statistics: the variance and the standard deviation. Both of these tell us an average distance of any observation in the data set from the mean of the distribution.

Standard deviation definition
Earlier, when we calculated the range, the answers were expressed in the same units as the data. For the variance, however, the units are the squares of the units of the data – for example, “squared dollars” or “dollars squared”. Squared dollars or dollars squared are not intuitively clear or easily interpreted. For this reason, we have to make a significant change in the variance to compute useful measure of deviation one that does not give us a problem with units of measure and thus is less confusing. According to the , definition of standard deviation, this measure is called the standard deviation, and it is the square root of the variance. The square root of 100 dollars squared is 10 dollars because we take the square root of both the value and the units in which it is measured. The standard deviation, then, is in units that are the same as the original data.

Let us now define standard deviation: The standard deviation is a numerical measure of the average variability of a data set around its mean. The standard deviation for a population is denoted by s (Greek lower case letter sigma) and standard deviation for a sample denoted by s.The mean deviation has a limitation that it ignores the sign of x -   in the general case of an observation x. The standard deviation gets over this limitation by squaring x -  . (x -  )2 is positive whether or not x -   is negative or positive. Note that population means data set comprising of 100% items under study, and sample means data set comprising of sample items drawn out of the population so that by studying the sample, inferences may be drawn about the population.

Sequences and Series- An introduction

Sequence:


Let us consider the following collection of numbers – 
(1) 28,2,25,27,--------
(2) 2,7,11,19,31,51, ---------
(3) 1,2,3,4,5,6, --------------
(4) 20.5,18.5,16.5,14.5,12.5,10.5, ------------
In (1) the numbers are not arranged in a particular order. In (2) the numbers are in ascending order but they do not obey any rule or law. It is, therefore not possible to indicate the number next to 51.
In (3) we find that by adding 1 to any number, we get the next number. So the number after 6 would be = 6+1 = 7.
In (4) if we subtract 2 from any number we get the number that follows. So here the number after 10.5 would be = 10.5-2 = 8.5
Under these circumstances, we say, the numbers in the collections (1) and (2) do not form sequences whereas the numbers in the collections (3) and (4) form sequences.
Definition: An ordered collection of numbers a1,a2,a3,a4,….. an,…… is called a sequence if according to some definite rule or law there is a definite value of an, called the term or element of the sequence, corresponding to any value of the natural number n.
Clearly the nth term of a sequence is a function of the positive integer n. If the nth term itself is also always an integer, then such a sequence is called an integer sequence.

Series:

An expression of the form a1+a2+a3+a4+….. +an+….. which is the sum of the elements of a sequence {an} is called a series.

If Sn = u1+u2+u3+….un, the Sn is called the sum to n terms (or the sum of first n terms) of the series and is denoted by the Greek letter sign ?.
Thus Sn = ?_(r=1)^n¦u_r

If a sequence or a series contains finite number of elements, it is called a finite sequence or series, otherwise they are called infinite sequences and series.

Progressions:

There are mainly three types of progressions –
(a) Arithmetic progression (A.P.): That means a sequence in which each term is obtained by adding a constant d to the preceding term. This constant ‘d’ is called the common difference of the arithmetic progression.
(b) Geometric progression (G.P.): If in a sequence of terms each term is constant multiple of the proceeding term, then the sequence is called a Geometric Progression (G.P.). The constant  multiplier is called the common ratio (r).
(c) Harmonic progression (H.P.): If each term of an A.P. is replaced by its reciprocal, then we get a harmonic progression.

type of polygons

Few names of polygons are as follows:

• Triangle or Trigon

This is a three-sided shape that having whole interior angle measurement as 180º.

• Quadrilateral or Tetragon

This is a four-sided shape that having whole inside angle measurement as 360º.

• Pentagon

This is a five-sided shape which contains the whole inside angle measurement as 540º.
The polygon is a closed path. The polygon has the different shapes. The shapes are depends on the number of sides. The Straight lines are form the polygon shapes. The polygons are having more number of straight lines to form the different polygons. Angles of the polygons are varied based on shape of the polygon.
The area of the regular polygon can be written as,
Area = S² N / 4 tan (pi / N).
Here, S = Length of any side, N = Number of side, Pi = 3.14.

Area of the Polygons

1) The given length of side:
Area Shape of polygon = S² N / 4 tan (Pi/N)
Here, S = Side length, N = Number of side, Pi = 3.14.
2) Given the radius(circum radius):
Area shape of polygon = (R² N sin (2Pi/N))/2.
Here, R = Radius of the polygon, N = Number of side, Pi = 3.14.
3) Given the apothem (In radius):
Area Shape of polygon = A² N tan (Pi/N).
Here, A = Apothem length, N = Number of sides.
4) Given the apothem and Length of a side:
Area shape of polygon = A* P / 2.
Here, A = Apothem length, P = Perimeter.

More about Polygon:

Basic diagrammatic representation for polygon is as follows:

Polygon- A polygon is a closed figure made by joining line segments, where each line segment intersects exactly two others.

Regular Polygon- A regular polygon is a polygon whose sides are all the same length, and whose angles are all the same.

Quadrilateral- A four-sided polygon. The sum of the angles of a quadrilateral is 360^o.

Rectangle- A four-sided polygon having all right angles. The sum of the angles of a rectangle is 360^o.

Square- A four-sided polygon having equal-length sides meeting at right angles. The sum of the angles of a square is 360^o.

Parallelogram- A four-sided polygon with two pairs of parallel sides. The sum of the angles of a parallelogram is 360^o.

Rhombus- A four-sided polygon having all four sides of equal length. The sum of the angles of a rhombus is 360^o.

Trapezoid- A four-sided polygon having exactly one pair of parallel sides. The two sides that are parallel are called the bases of the trapezoid. The sum of the angles of a trapezoid is 360^o.

Pentagon- A five-sided polygon. The sum of the angles of a pentagon is 540^o.

Hexagon- A six-sided polygon. The sum of the angles of a hexagon is 720^o.

Octagon- An eight-sided polygon. The sum of the angles of an octagon is 1080^o.

Nonagon- A nine-sided polygon. The sum of the angles of a nonagon is 1260^o.

Decagon- A ten-sided polygon. The sum of the angles of a decagon is 1440^o.

Convex- A figure is convex if every line segment drawn between any two points inside the figure lies entirely inside the figure. A figure that is not convex is called a concave figure.

Area of a square = side x side

= s x s

= s² sq units or units²

Area of a Rectangle = length x width

= l x w

= lw sq units or units²

Area of a Parallelogram= base x height

= b x h

= bh sq units or units²

Area of a Triangle = ½ x base x height

= ½ b h sq units or units²

Area of a Rhombus = base x height

= b x h

= bh sq units or unit²

Area of a Trapezoid = ½ (a+b)h sq units or units²

(Half of the sum of the lengths of the

Parallel sides times height)

Statistics: Bias and Sample Bias

In statistics we come across two types of errors, random errors and systematic errors. Random error is the error due to sampling variability or at times measurement precision. It occurs essentially in all quantitative studies and can be minimized to an extent but not avoided. We might wonder, What is Bias? Bias or Systematic error is a reproducible inaccuracy that produces a consistently false pattern of differences between observed (estimated) and true values. We get Definition Bias or definition of Bias as the systematic or average difference between the true value of the parameter and the experimental estimate value.

Bias Statistics or Statistical Bias is an error we cannot correct by repeating an experiment many times and averaging together the results, it is a directional error in an estimator.In a population which includes 50% males and 50% females, if we know that an important variable is the gender. Then the sample needs to include the same proportion. But if the sample includes 30% males then we can say that the results are likely biased as there are not enough responses from the male gender. This is how we know Sample Bias or in other words if the given sample is biased.

In statistics, Bias is used to refer the directional error in an estimator. Though we repeat the same experiment many times there would be some randomness existing.  By repeating an experiment we might see a slight variation in the estimation values. The bias is a systematic or average difference between the experimental estimate and the true value.

Examples of Bias
For example, if the national census could be completed online using the internet, then the sampling is said to be biased as only those people who could afford a computer and internet connection would be included and the people who cannot afford a computer or have the necessary skills to operate one will be excluded.

Jason was assigned by his editor to determine what most Americans think about the new law that will place a special tax on all electronic goods purchased and was told to mention in the survey form that he revenue returns collected from the tax would be made use of to enforce new online decency laws. Jason decided to use the email poll for convenience. In this poll 90% of those surveyed opposed the tax. Jason was quite surprised when 65% of all Americans voted for the taxes. So, online and call-in polls are particularly biased as the respondents are self-selected.

For example, a movie is released and a survey is done on the first day first show to know how people liked it. In the survey some say the movie was awesome and they all liked it and some say the movie was boring and they did not like it at all. Here ‘they’ might refer to only their group.

Inverse Function

What is an Inverse Function?

Inverse Function

In real life, did you ever undo the activity you or some other person has performed? If yes, then you have applied inverse function in your life. The inverse function is a function which will undo another function.  For example, let us consider that you have to call your friend using your mobile phone. When you wanted to dial to your friend, you will open the phone book, select his name and click the call button. What happens internally? The phone number of the corresponding name is retrieved and a call is established to that number. In the inverse way, what happens when your friend calls you? You get his name listed in the caller id. This is because; your friend’s phone number reaches your phone. The number gets converted into name and gets displayed. Thus, while calling your friend, the name gets converted into number. While receiving the call, the inverse of function happens and the number gets converted into the name.

However, the inverse of a function must result in the function itself i.e. assume that John is in your contact list and his number is 9904567345. If you call John from your phone book, then the call goes to 9904567345. In that case, when you receive a call back from 9904567345, it should be displayed as John in your phone and not some other name.

Here is another example for you: If a function represents the statement: “John is the father of Dave” then the inverse function will be: “Dave is the son of John”.

How to find Inverse Function?
Now that we know what the inverse of a function is, let us concentrate on how to find inverse function. Finding the inverse of a function can be demonstrated using the algebraic equation x = 4y + 3.

For finding inverse functions of x=4y+3, follow the steps given below:

Step 1: Move the + 3 on right side to the left side. Inverse of addition is subtraction. Thus when the +3 goes to the left side, it becomes -3. Thus the function will be evolved into x-3 = 4y.

Step 2: Now the number 4 has to be moved from right side to left side. Number 4 which is multiplied with y has to move to left side. Inverse of multiplication is division. Thus the 4 on the right hand side will perform division when moving to the left side. The function will now be transformed into (x-3)/4 = y.

Thus the inverse function of x=4y+3 is y=(x-3)/4.

Learn Exponential functions

Definition of Exponential functions: Exponential functions  are those function in which independent variable appear as an exponent .
exponential functions examples : y = 3x , f(x) = ex , y = 32x+5  are an example of exponential function.
Exponential function
Y = ax, where a is a positive real number and a ?0  is the most popular exponential function . It is an increasing function (as the value of x increasing the value of y increases ) when a>1, It is a decreasing function (as the value of x decreases the value of y decreases ) when a<1.
Derivative of exponential function :
We will use the following property to derivate  exponential function such as
  (ex) = ex

Least common multiple and Least common denominator

Least common multiple or LCM of two numbers is the smallest number that is multiple of both.
How to find the least common multiple?
Methods to find the LCM:
1. Prime factorization method – Following steps are followed to find LCM by prime factorization method:
• Find the factors of numbers whose LCM has to be obtained.
• Find the common factors of all the numbers.
• Find the factors that are not common.
• LCM is the product of common factors and the factors that are not common
LCM = (Product of common factors) X (Product of uncommon factors)
2. Common division method – Following steps are followed to find LCM by common division method: -
• Arrange numbers together separated by commas.
• Start with smallest prime number and keep on dividing till none of the numbers can further be divided.
• Multiply all the factors together to find the LCM.
The common division method is useful for finding the LCM of more than two numbers.
Least common denominator
Least common denominator is calculated for adding and subtracting the fractions. We cannot add or subtract any fraction before finding the least common denominator.
 How to find the least common denominator? (Finding the least common denominator)
Least common denominator finder
Suppose if we have two fractions such as 7/4 and 5/6.
To add these fractions, we need to find the least common denominator and o find the least common denominator of these two fractions, we find the least common multiple of their denominators i.e. LCM of 4 and 6.
4 = 2 X 2
6 = 2 X 3
2 is the only common factor and 2, 3 are the factors that are not common.
Product of common factors = 2
Product of factors that are not common = 2 X 3 = 6
LCM = (Product of common factors) X (Product of factors that are not common)
= (2) X (2 X 3) = 2 X 6 = 12
Hence the LCM of 4 and 6 is 12.
The least common denominator of 7/4 and 5/6 is 12
7/4 + 5/6 = 7*3/4*3 + 5*2/6*2 = 21/12 + 10/12 = 31/12

Properties of Real Numbers

What is a Real Number?
You can define real number as any valid number, be it whole number or rational number or irrational number. For example: 1, 1.234, 1/8, π, √7 are real numbers.

Properties of Real Numbers
There are certain properties that can be applied to all the real numbers. The different properties of real numbers are:

Cumulative Property
• Cumulative Property of Addition: This property of real numbers states that if there are two numbers, they can be added in any order. For example, 10 + 5 = 5 + 10

• Cumulative Property of Multiplication: This property states that the numbers can be multiplied in any order. For example, 10 X 5 = 5 X 10, both return the same value.

Associative Property
• Associative Property of Addition: If more numbers have to be added together, then you can associate any of them together in any way. For example, 10 + (5 + 2) = (10 + 5) + 2.

• Associative Property of Multiplication: If more numbers have to be multiplied together, then they can be associated in any way. For example, 10 X (5 X 2) = (10 X 5) X2.

Identity Property
• Identity Property of Addition: Any number added to zero will result in the number itself.  For example, 10 + 0 = 10.

• Identity Property of Multiplication: Any number added to one will result in the number itself. For example, 10 X 1 = 10.

Inverse Property
• Inverse Property of Addition: A positive number when added to its inverse results in zero. For example, 10 + (-10) = 0.

• Inverse Property of Multiplication: A number when multiplied by (1/same number) will result in 1. For example, 10 X (1 / 10) = 1.

Zero Property
Any number multiplied with zero results in zero. For example, 10 X 0 = 0

Density Property
 As per density property, it is always feasible to find a number existing between two real numbers. For example, between 10.1 and 10.2 you have a lot of numbers like 10.11, 10.12, and 10.13 and so on.

Distributive Property
Distributive property is applied when an expression includes addition and also multiplication. If a number is multiplied with a result of addition, then the multiplication has to be distributed over all the numbers participating in addition. For example, 2 X (5 + 10) = (2 X 5) + (2 X 10)

If you understand these properties clearly, then you can easily solve the algebra problems that include even complex expressions.

Derivatives of cotangent function

Derivative of cot:
Based on the above discussion we see that cot function exists (or is defined) only if sin(x) at that point is not equal to zero. Therefore for the derivative of cot function to exist, the following condition has to be met:
 Interval (a,b) should not contain n(pi) for any n Є Z, (Z = set of all integers). That is because, for x = n(pi), sin (x) = sin (n(pi)) = 0. And we already established that sin function cannot be equal to zero for cot function to exist at that point.

Derivative of cot x:
If (a,b) does not contain 

Assuming that sin and cos are differentiable and x ≠ n(pi), then sin x ≠ 0.


Proof for derivative of cotx:

The above derivation was using the quotient rule. We can also obtain the above form using the limit definition of derivative as follows:
Derivative of cot x (using limit definition):

Derivative of cot(-x):

(using chain rule, therefore multiplying by (d/dx) (-x) = -1)

= csc^2(x)

Improper Fractions

What is an improper fraction?
An improper fraction is a fraction in which the numerator, (the top number) is greater than the denominator (the bottom number).  Like in a fraction a/b, it is improper when a>b and b not zero.

For example, 5/3 is an improper fraction (5>3)
Improper fractions can be written as a mixed number, mixed number is a fraction in which we have a whole part and fraction part. 3 ½ is a mixed number, with 3 as the whole part and ½ , the fraction part
Let us convert a mixed numbers to improper fractions.

To convert a mixed number to improper fraction, we first find the product of the whole part and the denominator and then add the numerator to this product. This gives us the numerator of the improper fraction, the denominator remains the same

Convert  the mixed number, 5 ¾ to an improper fraction
(5=whole part, 3=numerator, 4=denominator)

Improper Fraction example

we find the product of the whole part and the denominator
Product = (whole part x denominator) = (5 x 4) = 20
then, we add the numerator to the product
      = 20 +3 = 23 (numerator)
While converting, the denominator remains the same
So, the improper fraction will be 23/4

Converting improper fraction to mixed number
Example: Convert the improper fraction, 8/3 to a mixed number
To convert, we need to divide the improper fraction using the long division method. The quotient will be the whole part, the remainder the numerator and the denominator remains the same
When we divide 8 with 3, we get
Quotient = 2 and remainder = 2
So, the required improper fraction would be 2 ⅔      
(2 is the whole part, ⅔ is the fraction part)

Improper fraction to mixed number
To understand the converting of an improper fraction to a mixed number, let us take a look at the example given below:
Convert the improper fraction 24/5 to mixed number
Divide 24 with 5 using the long division method
24 ÷ 5 = 4 (quotient) Remainder = 4
The mixed number is written as 4 4/5

Fraction and its types

Let's learn all about fractions in today's post.

What is a fraction? A fraction is a rational number having one numerator and a denominator.

What does fraction represents? Fractions represents ratio, decimals and percentages.

Types of fractions: There are three types of fractions: proper fraction, improper fraction and mixed fraction.

Proper fraction: A fraction where numerator is smaller than the denominator.
Improper fraction: A fraction where denominator is smaller than the numerator.
Mixed fraction: A fraction formed of a whole number and a fraction.

Fraction operations: There are different operations involved with fractions: ordering fractions, comparing fractions, reducing fractions, adding, subtracting multiplying and dividing fractions and so on.

For more help connect to an online tutor and get your help. Not just fractions help but you can get help with every concept such as geometry help from geometry tutors.

Do post your comments.